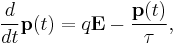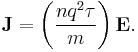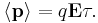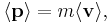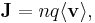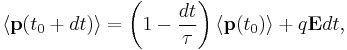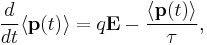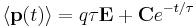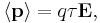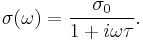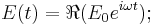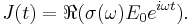Drude model

The Drude model of electrical conduction was proposed in 1900^[1]^[2] by Paul Drude to explain the transport properties of electrons in materials (especially metals). The model, which is an application of kinetic theory, assumes that the microscopic behavior of electrons in a solid may be treated classically and looks much like a pinball machine, with a sea of constantly jittering electrons bouncing and re-bouncing off heavier, relatively immobile positive ions.

The two most significant results of the Drude model are an electronic equation of motion,

$\frac{d}{dt}\mathbf{p}(t) = q\mathbf{E} - \frac{\mathbf{p}(t)}{\tau},$

and a linear relationship between current density $J$ and electric field $E$ ,

$\mathbf{J} = \left( \frac{n q^2 \tau}{m} \right) \mathbf{E}.$

Here $t$ is the time and $p$ , $q$ , $n$ and $m$ , and $\tau$ are respectively an electron's momentum, charge, number density, mass, and mean free time between ionic collisions. The latter expression is particularly important because it explains in semi-quantitative terms why Ohm's Law, one of the most ubiquitous relationships in all of electromagnetism, should be true.^[3]^[4]^[5]

The model was extended in 1905 by Hendrik Antoon Lorentz (and hence is also known as the Drude–Lorentz model) and was supplemented with the results of quantum theory in 1933 by Arnold Sommerfeld and Hans Bethe.

1 Assumptions
2 Explanations
- 2.1 DC field
- 2.2 Time-varying analysis
3 Accuracy of the model
4 See also
5 References

Assumptions

The Drude model considers the metal to be formed of a mass of positively-charged ions from which a number of "free electrons" were detached. These may be thought to have become delocalized when the valence levels of the atom came in contact with the potential of the other atoms.^[6]

Notwithstanding the origin of such free electrons from the contact of different potentials, the Drude model neglects any long-range interaction between the electron and the ions and assumes that the electrons do not interfere with each other. The only possible interaction is the instantaneous collision between a free electron and an ion, which happens with a fixed probability per unit time.^[6]

The Drude model is a purely classical model, and treats both electrons and ions as solid spheres.

Explanations

DC field

The simplest analysis of the Drude model assumes that electric field 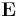$\mathbf{E}$ is both uniform and constant, and that the thermal velocity of electrons is sufficiently high such that they accumulate only an infinitesimal amount of momentum 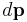$d\mathbf{p}$ between collisions, which occur on average every $\tau$ seconds.^[3]

Then an electron isolated at time $t$ will on average have been traveling for time $\tau$ since its last collision, and consequently will have accumulated momentum

$d\langle\mathbf{p}\rangle = q \mathbf{E} \tau.$

During its last collision, this electron will have been just as likely to have bounced forward as backward, so all prior contributions to the electron's momentum may be ignored, resulting in the expression

$\langle\mathbf{p}\rangle = q \mathbf{E} \tau.$

Substituting the relations

$\langle\mathbf{p}\rangle = m \langle\mathbf{v}\rangle,$

$\mathbf{J} = n q \langle\mathbf{v}\rangle,$

results in the formulation of Ohm's Law mentioned above:

$\mathbf{J} = \left( \frac{n q^2 \tau}{m} \right) \mathbf{E}.$

Time-varying analysis

The dynamics may also be described by introducing an effective drag force. At time 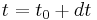$t=t_0%2Bdt$ the average electron's momentum will be

$\langle\mathbf{p}(t_0%2Bdt)\rangle=\left( 1 - \frac{dt}{\tau} \right) \langle\mathbf{p}(t_0)\rangle %2B q\mathbf{E}dt,$

because, on average, 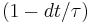$( 1 - dt/\tau )$ electrons will not have experienced another collision, and the ones that have will contribute to the total momentum to only a negligible order.^[7]

With a bit of algebra, this results in the differential equation

$\frac{d}{dt}\langle\mathbf{p}(t)\rangle = q\mathbf{E} - \frac{\langle\mathbf{p}(t)\rangle}{\tau},$

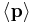where $\langle\mathbf{p}\rangle$ denotes average momentum, m the effective mass and q the charge of the electrons. This, which is an inhomogeneous differential equation, may be solved to obtain the general solution of

$\langle\mathbf{p}(t)\rangle = q \tau \mathbf{E} %2B \mathbf{C} e^{-t/\tau}$

for p(t). The steady state solution (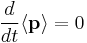 $\frac{d}{d t}\langle\mathbf{p}\rangle = 0$ ) is then

$\langle\mathbf{p}\rangle = q \tau \mathbf{E},$

As above, average momentum may be related to average velocity and this in turn may be related to current density,

$\langle\mathbf{p}\rangle = m \langle\mathbf{v}\rangle,$

$\mathbf{J} = n q \langle\mathbf{v}\rangle,$

and the material can be shown to satisfy Ohm's Law with a DC-conductivity 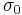$\, \sigma_0$ :

$\mathbf{J} = \left( \frac{n q^2 \tau}{m} \right) \mathbf{E}.$

The Drude model can also predict the current as a response to a time-dependent electric field with an angular frequency 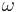$\, \omega$ , in which case

$\sigma(\omega) = \frac{\sigma_0}{1 %2B i\omega\tau}.$

Here it is assumed that

$E(t) = \Re(E_0 e^{i\omega t});$

$J(t) = \Re(\sigma(\omega) E_0 e^{i\omega t}).$

In other conventions, 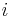$\, i$ is replaced by 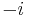$\, -i$ in all equations. The imaginary part indicates that the current lags behind the electrical field, which happens because the electrons need roughly a time 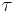$\, \tau$ to accelerate in response to a change in the electrical field. Here the Drude model is applied to electrons; it can be applied both to electrons and holes; i.e., positive charge carriers in semiconductors. The curves for 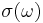$\sigma(\omega)$ are shown in the graph.

Accuracy of the model

This simple classical Drude model provides a very good explanation of DC and AC conductivity in metals, the Hall effect, and thermal conductivity (due to electrons) in metals near room temperature. The model also explains the Wiedemann-Franz law of 1853. However, it greatly overestimates the electronic heat capacities of metals. In reality, metals and insulators have roughly the same heat capacity at room temperature. Although the model can be applied to positive (hole) charge carriers, as demonstrated by the Hall effect, it does not predict their existence.

One note of trivia surrounding the theory is that in his original paper Drude made a conceptual error, estimating electrical conductivity to in fact be only half of what it classically should have been.^[8]

References

^ Drude, Paul (1900). "Zur Elektronentheorie der metalle". Annalen der Physik 306 (3): 566. Bibcode 1900AnP...306..566D. doi:10.1002/andp.19003060312. http://www3.interscience.wiley.com/cgi-bin/fulltext/112485959/PDFSTART.
^ Drude, Paul (1900). "Zur Elektronentheorie der Metalle; II. Teil. Galvanomagnetische und thermomagnetische Effecte". Annalen der Physik 308 (11): 369. Bibcode 1900AnP...308..369D. doi:10.1002/andp.19003081102. http://www3.interscience.wiley.com/cgi-bin/fulltext/112485893/PDFSTART.
^ ^a ^b Neil W. Ashcroft; N. David Mermin (1976). Solid State Physics. Saunders College. pp. 6–7. ISBN 0-030839-939.
^ Edward M. Purcell (1965). Electricity and Magnetism. McGraw-Hill. pp. 117–122. ISBN 978-0-070049-086.
^ David J. Griffiths (1999). Introduction to Electrodynamics. Prentice-Hall. pp. 289. ISBN 978-0138053260.
^ ^a ^b Neil W. Ashcroft; N. David Mermin (1976). Solid State Physics. Saunders College. pp. 2–3. ISBN 0-030-83993-9.
^ Neil W. Ashcroft; N. David Mermin (1976). Solid State Physics. Saunders College. pp. 11. ISBN 0-030-83993-9.
^ Neil W. Ashcroft; N. David Mermin (1976). Solid State Physics. Saunders College. pp. 23. ISBN 0-03-083993-9.

Atomic Models

Single atoms	Dalton model (Billiard Ball Model) · Thomson model (Plum Pudding Model) · Lewis model (Cubical Atom Model) · Nagaoka model (Saturnian Model) · Rutherford model (Planetary Model) · Bohr model (Rutherford–Bohr Model) · Bohr–Sommerfeld model (Refined Bohr Model) · Gryziński model (Free-fall Model) · Schrodinger model (Electron Cloud Model)

Atoms in solids	Drude model · Free electron model · Nearly-free electron model · Band structure · Density functional theory

Atoms in liquids	Liquid helium

Atoms in gases	Noble gas · Nascent hydrogen

Scientists	Felix Bloch · Niels Bohr · John Dalton · Paul Drude · Irving Langmuir · Gilbert N. Lewis · Hantaro Nagaoka · Ernest Rutherford · Erwin Schrödinger · Arnold Sommerfeld · J. J. Thomson

Book:Atomic models · Category:Atoms · Portal:Physics / Chemistry

Drude model

Contents

Assumptions

Explanations

DC field

Time-varying analysis

Accuracy of the model

See also

References